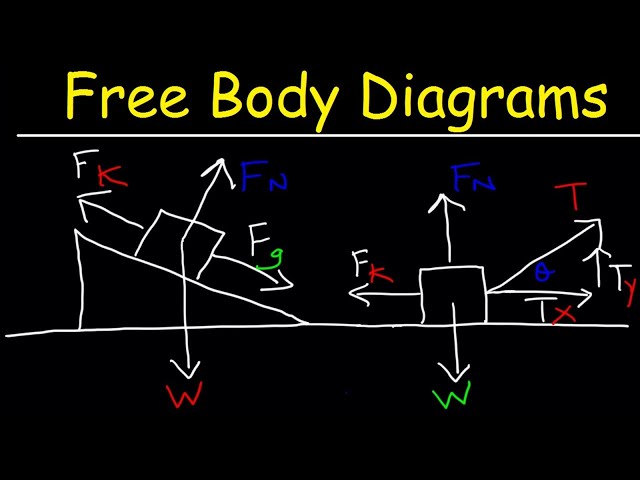
Free Body Diagram Examples: A Comprehensive Guide for Beginners

Free Body Diagram Examples

A free body diagram is a graphical representation of all the forces acting on an object. It is a useful tool for understanding how objects move and interact with each other. Free body diagrams can be used to solve a variety of problems in physics, including problems involving motion, equilibrium, and forces.

There are many different types of free body diagrams, but they all share some common features. First, a free body diagram always includes a representation of the object that is being analyzed. This representation can be as simple as a point or as complex as a detailed drawing. Second, a free body diagram includes vectors that represent the forces acting on the object. These vectors are drawn with arrows, and the length of each arrow represents the magnitude of the force. Third, a free body diagram includes a coordinate system. This coordinate system is used to define the direction of the forces.

Free body diagrams can be used to solve a variety of problems in physics. For example, free body diagrams can be used to determine the acceleration of an object, the tension in a rope, or the force of friction between two surfaces. Free body diagrams can also be used to analyze the stability of structures and to design machines.

Benefits of using free body diagrams:

• Free body diagrams help to visualize the forces acting on an object.
• Free body diagrams can be used to solve a variety of problems in physics.
• Free body diagrams can help to improve understanding of how objects move and interact with each other.

Steps for creating a free body diagram:

1. Draw a representation of the object.
2. Identify all of the forces acting on the object.
3. Draw vectors to represent the forces.
4. Label the vectors with the magnitude and direction of the forces.
5. Choose a coordinate system.

Here are some examples of free body diagrams:

• A free body diagram of a block on a ramp
• A free body diagram of a car
• A free body diagram of a person jumping

Free body diagrams are a powerful tool for understanding how objects move and interact with each other. They can be used to solve a variety of problems in physics, and they can help to improve understanding of the world around us.

Free Body Diagram Examples

Free body diagrams (FBDs) provide a visual representation of the forces acting on an object. They are a fundamental tool in mechanics, used to analyze motion, equilibrium, and forces. Here are six key aspects of FBDs:

• Graphical representation: FBDs represent forces as vectors, making it easy to visualize their direction and magnitude.
• Object isolation: FBDs isolate an object from its surroundings, focusing only on the forces acting directly on it.
• Force identification: FBDs help identify all the forces acting on an object, even those that may not be obvious.
• Problem-solving tool: FBDs are used to solve a wide range of physics problems, from simple equilibrium to complex dynamics.
• Conceptual understanding: FBDs enhance conceptual understanding of how forces interact and affect motion.
• Engineering applications: FBDs are essential in engineering design and analysis, helping engineers predict and control the behavior of structures and machines.

In summary, FBDs are versatile and powerful tools that provide a clear understanding of forces and their effects. They are used in various fields, from physics and engineering to biomechanics and sports science. By understanding these key aspects, individuals can effectively utilize FBDs to analyze and solve problems related to motion, equilibrium, and forces.

Graphical representation

Graphical representation is a key aspect of free body diagrams (FBDs). By representing forces as vectors, FBDs provide a clear and intuitive way to visualize their direction and magnitude. This graphical approach offers several advantages in the context of free body diagram examples:

• Simplified visualization: Vectors are graphical representations that simplify the visualization of forces. They have both magnitude and direction, allowing for easy understanding of the force’s strength and orientation.
• Clear force identification: Vectors make it easy to identify and distinguish different forces acting on an object. Each vector represents a specific force, providing a clear visual representation of the force system.
• Convenient manipulation: Vectors can be easily manipulated graphically, making it convenient to analyze and solve problems related to forces. For example, vectors can be added, subtracted, or resolved into components.
• Enhanced problem-solving: The graphical representation of forces as vectors enhances problem-solving capabilities. It allows for quick identification of the net force, determination of equilibrium conditions, and analysis of force interactions.

In summary, the graphical representation of forces as vectors in FBDs provides a powerful tool for visualizing, understanding, and analyzing forces. It simplifies the comprehension of force systems, aids in problem-solving, and enhances the overall effectiveness of free body diagrams.

Object isolation

In the context of free body diagram examples, object isolation is crucial for understanding the forces acting on a specific object and analyzing its motion or equilibrium. FBDs isolate the object of interest from its surroundings, allowing for a focused examination of the forces directly affecting it.

• Simplification of analysis: By isolating the object, FBDs simplify the analysis process by eliminating the need to consider external forces or interactions with other objects. This isolation enables a clear understanding of the forces directly responsible for the object’s behavior.
• Identification of key forces: Object isolation helps identify the key forces acting on the object. By excluding external influences, FBDs allow for the determination of the forces that are most relevant to the object’s motion or equilibrium.
• Enhanced accuracy: Isolating the object minimizes the risk of overlooking or misinterpreting forces that may be present in the surroundings. This focus on the direct forces acting on the object enhances the accuracy of the analysis and the resulting free body diagram.
• Applicability to various scenarios: The principle of object isolation is applicable to a wide range of free body diagram examples, from simple objects like blocks on an inclined plane to complex systems like vehicles or structures. This versatility makes it a fundamental concept in mechanics and engineering.

In summary, object isolation in free body diagrams is essential for isolating and analyzing the forces acting directly on the object of interest. It simplifies the analysis, enhances accuracy, and provides a clear understanding of the forces responsible for the object’s motion or equilibrium.

Force identification

Force identification is a crucial component of free body diagram examples. It involves identifying all the forces acting on an object, including those that may not be immediately apparent. This process is essential for accurately representing the forces that influence the object’s motion or equilibrium.

In many real-life scenarios, forces acting on an object can be subtle or indirect. For instance, when a book rests on a table, the force of gravity pulls the book downward, while the normal force exerted by the table pushes the book upward. These forces may not be readily noticeable, but they are crucial for understanding why the book remains stationary.

Free body diagrams help identify these hidden forces by providing a systematic approach to analyzing all possible forces acting on an object. By considering every potential force, including friction, tension, buoyancy, and electromagnetic forces, FBDs ensure a comprehensive understanding of the forces that govern the object’s behavior.

The practical significance of force identification in free body diagrams is evident in various fields, including engineering, physics, and biomechanics. Engineers use FBDs to design structures that can withstand specific forces, such as bridges that can the weight of vehicles and wind loads. Physicists employ FBDs to analyze the motion of objects, such as projectiles and rockets, by identifying all the forces that influence their trajectory.

In conclusion, force identification is a fundamental aspect of free body diagram examples. It involves identifying all the forces acting on an object, even those that may not be obvious. This process is essential for accurately representing the forces that influence the object’s motion or equilibrium, and it has practical applications in various fields.

Problem-solving tool

Within the realm of “free body diagram examples,” the problem-solving capabilities of FBDs hold immense significance. They empower physicists and engineers to address a diverse array of physics problems, encompassing both static and dynamic scenarios.

• Equilibrium analysis:

  FBDs excel in analyzing equilibrium situations, where the net force acting on an object is zero. By identifying and balancing all forces acting on an object, FBDs help determine whether an object is at rest or moving with constant velocity.

• Motion analysis:

  FBDs extend their utility to problems involving motion. By applying Newton’s laws of motion, FBDs enable the calculation of acceleration, velocity, and displacement of objects under the influence of various forces.

• Dynamics of rigid bodies:

  FBDs play a crucial role in analyzing the dynamics of rigid bodies, such as rotational motion and torque. By considering the forces and moments acting on a rigid body, FBDs aid in predicting its angular acceleration and angular velocity.

• Complex systems analysis:

  The versatility of FBDs extends to complex systems involving multiple interacting objects. By constructing FBDs for each individual object and considering the forces between them, engineers can analyze the overall dynamics of the system.

In summary, “free body diagram examples” serve as a testament to the problem-solving prowess of FBDs. They facilitate the analysis of equilibrium, motion, and dynamics, empowering scientists and engineers to gain insights into the behavior of objects under the influence of forces.

Conceptual understanding

Within the realm of “free body diagram examples,” the role of FBDs in promoting conceptual understanding of force interactions and their impact on motion takes center stage. FBDs provide a visual representation of forces acting on an object, allowing learners to grasp the interplay of forces and their consequences.

• Visualization of force interactions:

  FBDs make visible the often-invisible forces that govern an object’s motion. By representing forces as vectors, FBDs illustrate the direction and magnitude of each force, aiding in the visualization of force interactions.

• Cause-and-effect relationships:

  FBDs establish a clear connection between forces and their effects on motion. By analyzing the forces acting on an object, students can deduce the object’s acceleration, velocity, and trajectory, reinforcing the cause-and-effect relationships between forces and motion.

• Equilibrium and stability:

  FBDs play a crucial role in understanding equilibrium and stability. By identifying the forces that balance each other, FBDs illustrate the conditions necessary for an object to remain at rest or in uniform motion.

• Real-life applications:

  FBDs extend beyond theoretical concepts and find applications in diverse fields. From analyzing the forces acting on a bridge to understanding the dynamics of a sports car, FBDs provide a practical framework for comprehending force interactions and their implications in the real world.

In summary, “free body diagram examples” serve as valuable tools for fostering a deep conceptual understanding of force interactions and their impact on motion. Through visualization, cause-and-effect analysis, and real-life applications, FBDs empower learners to grasp the intricacies of force dynamics and their consequences in the physical world.

Engineering applications

Within the realm of “free body diagram examples,” the engineering applications of FBDs hold paramount importance. FBDs serve as indispensable tools for engineers, enabling them to predict and control the behavior of structures and machines.

FBDs provide a systematic framework for analyzing the forces acting on an engineering structure or machine. By identifying and representing all external and internal forces, engineers can determine the stresses, strains, and deformations that the structure or machine will experience under various loading conditions.

This understanding is crucial for ensuring the safety and reliability of engineering designs. For instance, in designing a bridge, engineers use FBDs to analyze the forces exerted by traffic, wind, and seismic activity. This analysis helps them determine the appropriate materials and structural elements to ensure that the bridge can withstand these forces and remain stable.

In addition to structural analysis, FBDs are also essential for analyzing the dynamics of machines. By considering the forces acting on a machine’s components, engineers can predict its motion, acceleration, and torque. This information is critical for optimizing machine performance, efficiency, and longevity.

The practical significance of FBDs in engineering applications cannot be overstated. They empower engineers to design structures and machines that are safe, efficient, and reliable. From towering skyscrapers to high-speed trains, FBDs play a vital role in shaping the built environment and advancing technological progress.

In the realm of physics and engineering, free body diagrams (FBDs) serve as powerful tools for analyzing the forces acting on objects. FBDs provide a simplified, graphical representation of these forces, enabling a deeper understanding of an object’s motion and equilibrium.

FBDs are constructed by isolating an object from its surroundings and identifying all external forces that act upon it. These forces may include gravity, friction, tension, normal force, and applied forces. By representing each force as a vector, FBDs provide a clear visual representation of the direction and magnitude of the forces.

The significance of FBDs lies in their ability to simplify complex force systems and facilitate problem-solving. By isolating the object of interest and focusing solely on the forces acting on it, FBDs allow us to analyze the object’s motion and equilibrium more effectively. This approach is particularly useful in engineering design and analysis, where understanding the forces acting on a structure or machine is crucial for ensuring its stability and performance.

Throughout this article, we will delve into the intricacies of FBDs, exploring their applications, benefits, and step-by-step guidelines for creating them. We will also examine real-world examples of FBDs, showcasing their practical use in various fields.

FAQs on Free Body Diagrams

Free body diagrams (FBDs) are widely used in physics and engineering to analyze the forces acting on objects. Here, we address some commonly asked questions about FBDs to enhance understanding and dispel any misconceptions:

Question 1: What is the purpose of a free body diagram?

Answer: An FBD is a graphical representation of all the forces acting on an object. It helps visualize the forces and their directions, aiding in the analysis of an object’s motion and equilibrium.

Question 2: How do I create a free body diagram?

Answer: To create an FBD, isolate the object of interest and identify all external forces acting on it. Represent each force as a vector, indicating its direction and magnitude.

Question 3: What are some common mistakes when drawing FBDs?

Answer: Common mistakes include forgetting to include all forces (e.g., friction, tension), drawing forces in the wrong direction, and neglecting to label the forces and axes.

Question 4: How can FBDs be used in problem-solving?

Answer: FBDs help simplify complex force systems by isolating the object and focusing on the forces acting on it. This enables the application of Newton’s laws of motion and equilibrium equations to analyze the object’s behavior.

Question 5: Are FBDs only used in physics and engineering?

Answer: No, FBDs find applications in various fields, including biomechanics, sports science, and architecture, where understanding force interactions is crucial.

Final Thought: Free body diagrams are powerful tools for understanding the forces acting on objects. By mastering the concepts and applications of FBDs, we enhance our ability to analyze and solve problems involving motion and equilibrium.

Transition to the Next Section: Let’s explore some real-world examples of free body diagrams to further solidify our understanding.

Conclusion

Throughout this exploration of “free body diagram examples,” we have gained a deeper understanding of these powerful tools. FBDs provide a simplified and visual representation of the forces acting on an object, enabling us to analyze its motion and equilibrium more effectively.

By isolating the object of interest and focusing solely on the external forces acting upon it, FBDs allow us to visualize the direction and magnitude of these forces. This approach not only enhances our conceptual understanding but also facilitates problem-solving in various fields, including physics, engineering, biomechanics, and architecture.

As we continue to explore the realm of mechanics, FBDs will remain indispensable tools for analyzing force interactions and predicting the behavior of objects. By mastering the concepts and applications of FBDs, we empower ourselves to tackle complex problems and contribute to advancements in science, engineering, and beyond.

Youtube Video: